

 Teorie conformi 1 : nozioni base
Teorie conformi 1 : nozioni base
Trasformazioni conformi in uno spazio (pseudo-)riemannaniano D-dimensionale:


 Teorie conformi 1 : nozioni base
Teorie conformi 1 : nozioni base


Nel caso D=2 dobbiamo distinguere tra gruppo
conforme LOCALE e
GLOBALE
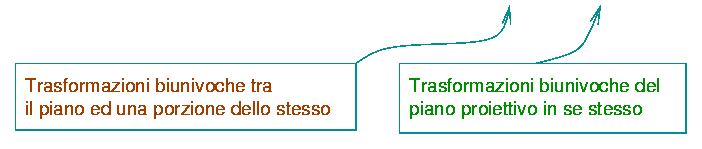
Si consideri
per primo il piano euclideo (p=2,q=0).
Conviene fare
uso delle coordinate complesse:

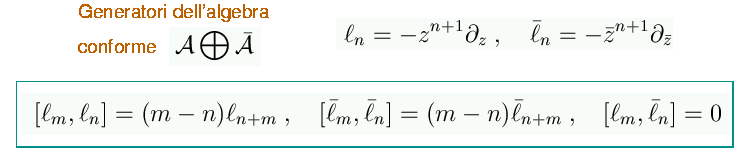
Sul
piano proiettivo, o sfera di Riemann, un campo vettoriale analitico![]()

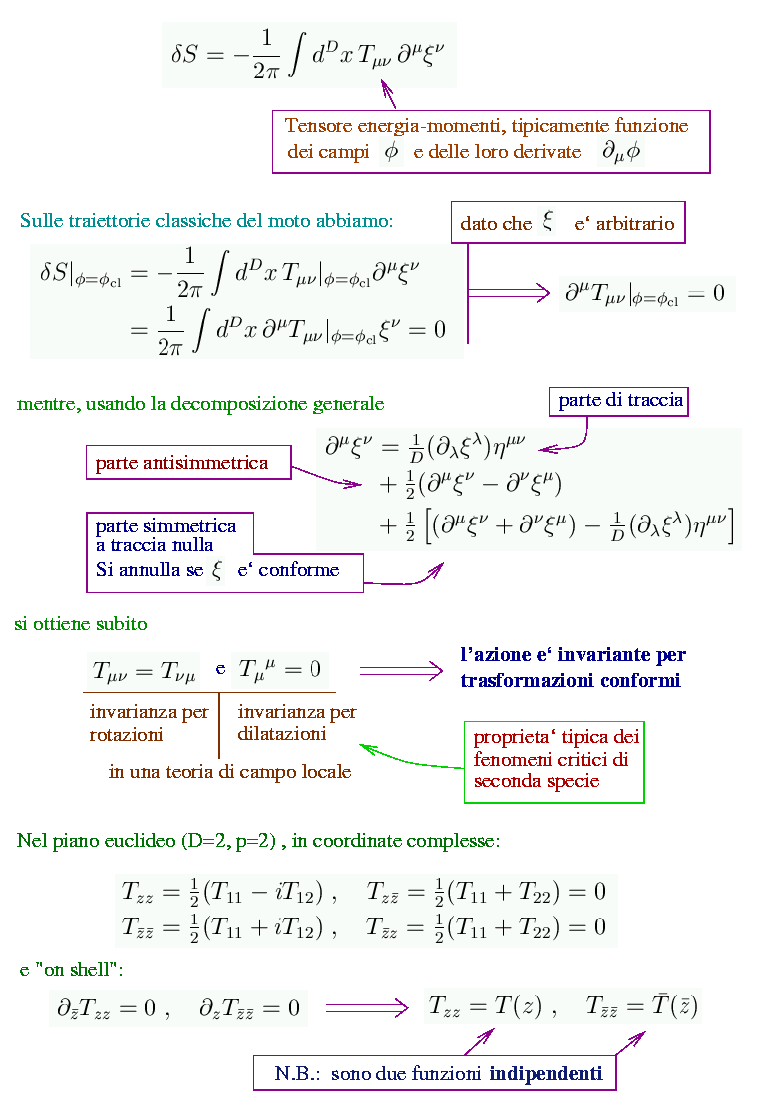
In una teoria di campo locale su uno spazio (pseudo-)euclideo D-dimensionale
con
azione S invariante per traslazione, la variazione
di
S
si
scrive ![]()
Nella
formulazione funzionale euclidea di una teoria quantistica di campo,
le funzioni di
correlazione
si scrivono:
Dato che il valore di un integrale resta immutato cambiando variabili di integrazione, si
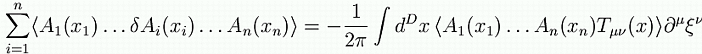


 Quindi
l'invarianza conforme fissa le seguenti forme per le funzioni di correlazione
Quindi
l'invarianza conforme fissa le seguenti forme per le funzioni di correlazione


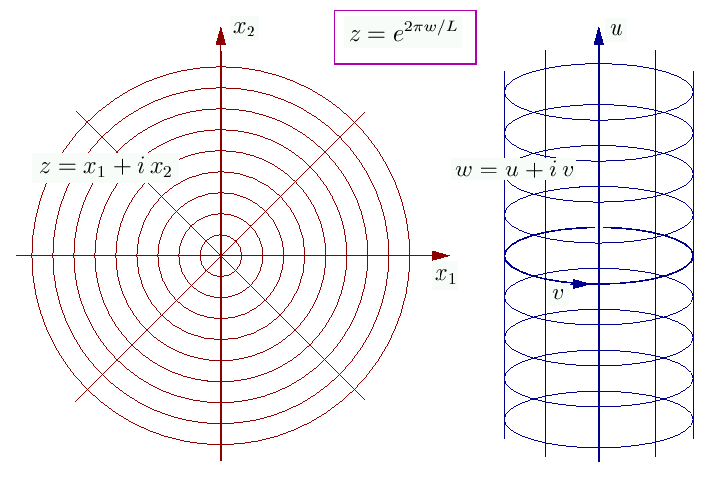
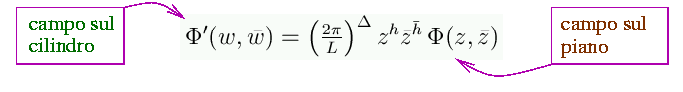
il che implica, ad esempio, per la funzione a due punti sul cilindro ![]()



