CFT 2

Teorie conformi 2 : ruolo del tensore energia-impulso

    In una QFT euclidea bidimensionale, la simmetria conforme rispetto al gruppo locale si esprime
    attraverso una forma particolare di identita` di Ward , ottenuta a partire dalle identita` relative
    a generiche variazioni locali dei campi fondamentali, vale a dire:

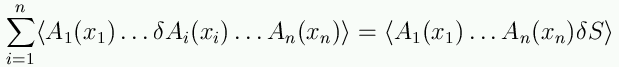
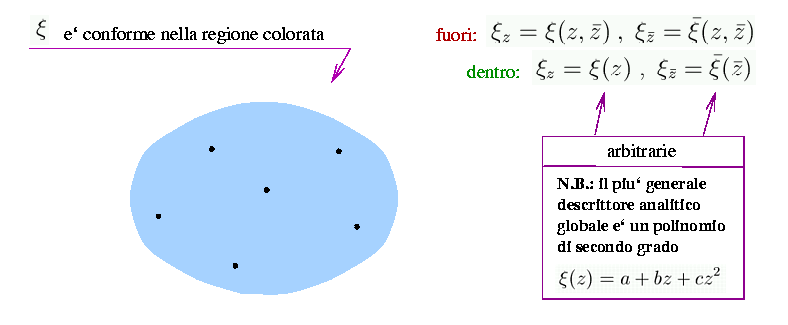
In coordinate complesse abbiamo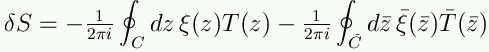

per cui si ottengono identita` indipendenti per i due tipi, olomorfo e antiolomorfo, di trasformazioni
conformi (cioe` )

avendo sfruttato la possibilita` di deformare opportunamente il contorno di integrazione all'interno
della regione di analiticita` (o antianaliticita`). In forma compatta possiamo scrivere

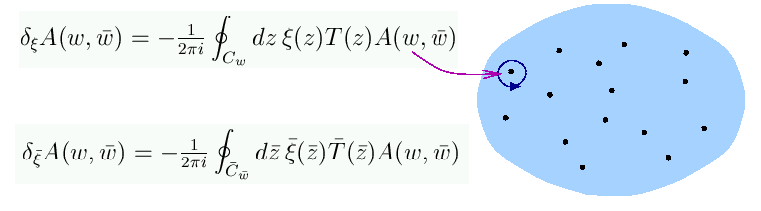
    D'ora in poi possiamo restringere l'attenzione alle sole trasformazioni olomorfe. Le formule per
    quelle antiolomorfe si ottengono in modo ovvio.

    Ad esempio, nel caso della mappa conforme tra piano e cilindro   abbiamo