L'approccio di Affleck e Ludwig allo studio dell'effetto Kondo si basa su due punti fondamentali:

Separazione dei gradi di liberta` elettronici relativi alla carica, allo spin ed ai diversi canali.
Trasformazione dell'interazione con l'impurezza in particolari condizioni al contorno conforme -invarianti per il campo elettronico.

Riprendiamo in esame l'Hamiltoniana di Kondo

Dalla mappa tra piano e cilindro ricaviamo ora

e la separazione tra i gradi di liberta` relativi ai due sottogruppi e` resa esplicita dalla bosonizzazione nonabeliana

   Tuttavia questa non e` la separazione giusta in previsione dell'effetto dell'interazione,
    la quale riduce la simmetria a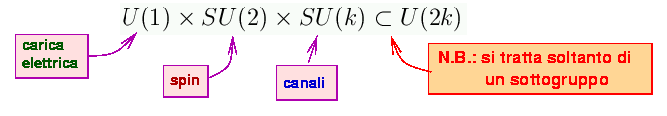
    Le relative correnti sono:

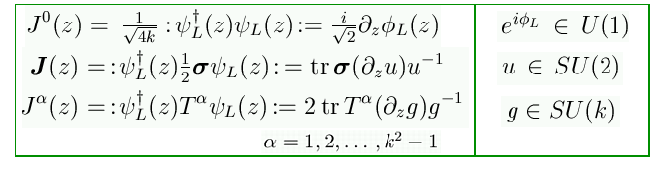
    E` importante osservare che le correnti nonabeliane non possono essere rinormalizzate liberamente
    come quella abeliana, dato il termine con le costanti di struttura nell'OPE
    Ne consegue che la SU(2) Kac-Moody algebra ha livello k, mentre quella di SU(k) ha livello 2.

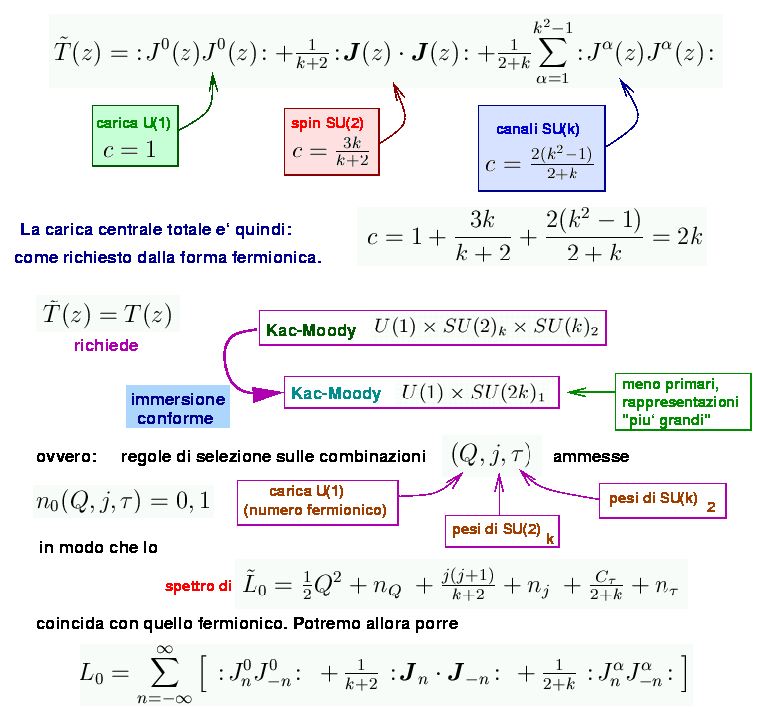
Consideriamo ora il tensore energia-momento alla Sugawara: